Η εντροπία πληροφοριών του Shannon

Έστω πως θέλουμε να κωδικοποιήσουμε την έκβαση ενός γεγονότος (πχ να στείλουμε σε έναν φίλο μας μήνυμα για το αν πέρασε το μάθημα της τεχνικής υδρολογίας). Είναι δυνατόν να του στείλουμε τις φράσεις «Πέρασες το μάθημα» και «Δεν πέρασες το μάθημα» αναλόγως με την έκβαση του συμβάντος. Εναλλακτικά είναι δυνατόν να του απαντήσουμε με ένα δυαδικό ψηφίο (bit): 1 εάν πέρασε το μάθημα και 0 εάν κόπηκε. Στην πρώτη περίπτωση το μήνυμα περιέχει 136 ή 168 bits πληροφορίας (8 bits ανά χαρακτήρα) ενώ στην δεύτερη περίπτωση περιέχει μόνο 1 bit. Άρα η απάντηση στο ερώτημα κωδικοποιείται βέλτιστα με 1 bit πληροφορίας.

Ειδικότερα εάν ένα συμβάν έχει Ν ισοπίθανες εκβάσεις, έχει αβεβαιότητα ίση με i bits όπου i=log₂N. Συνεπώς απαιτούνται i bits πληροφορίας για κωδικοποιηθεί βέλτιστα η τελική έκβαση και να επιλυθεί η αβεβαιότητα. Στο παραπάνω παράδειγμα όπου υπάρχουν 2 πιθανές εκβάσεις (πέρασε το μάθημα ή όχι), η κατανομή μάζας πιθανότητας έχει αβεβαιότητα ίση με i=log₂2=1 bit και συνεπώς η απάντηση που θα «επιλύσει» την αβεβαιότητα αυτή πρέπει να περιέχει 1 bit πληροφορίας.

Έπειτα, στην περίπτωση που ο φίλος μας αναρωτιόταν εάν πέρασε την τεχνική υδρολογία και την υδραυλική, τότε υπάρχουν 4 πιθανές απαντήσεις στο ερώτημα του: 11 (πέρασε και τα 2 μαθήματα), 10 (πέρασε μόνο την υδρολογία), 01 (πέρασε μόνο την υδραυλική) και 00 (δεν πέρασε κανένα μάθημα). Παρατηρούμε πως αυτή την φορά χρησιμοποιήθηκαν 2 δυαδικά ψηφία. Το 1ο κωδικοποιεί το αποτέλεσμα της υδρολογίας ενώ το 2ο το αποτέλεσμα της υδραυλικής. Συνεπώς το ερώτημα του έχει 2 bits αβεβαιότητας (ή ακριβέστερα η συνάρτηση μάζας πιθανότητας έχει αβεβαιότητα ίση με 2 bits) με αποτέλεσμα να απαιτούνται 2 bits πληροφορίας για την κωδικοποίηση της έκβασης. Πράγματι i=log₂4=2 bits.

Στην γενικότερη περίπτωση, ένα συμβάν έχει μη ισοπίθανες εκβάσεις. Αν κάθε έκβαση x έχει πιθανότητα p(x) να συμβεί (δηλαδή η συνάρτηση p(x) είναι η συνάρτηση μάζας πιθανότητας) τότε η εντροπία (αβεβαιότητα) του συμβάντος είναι ίση με i όπου

Ας εξετάσουμε πάλι το παράδειγμα με τις 2 εκβάσεις (η ερώτηση μόνο για το μάθημα της υδρολογίας). Εάν ο φίλος μας γνωρίζει πως η πιθανότητα να περάσει το μάθημα της υδρολογίας είναι 3/4 (75%) και η πιθανότητα να κοπεί είναι 1/4 (25%) τότε η αβεβαιότητα είναι

Παρατηρούμε πως στην περίπτωση των μη ισοπίθανων εκβάσεων το ερώτημα έχει μικρότερη αβεβαιότητα (0.81 bits έναντι του 1 bit), δηλαδή η αντίστοιχη συνάρτηση μάζας πιθανότητας έχει μικρότερη εντροπία. Άρα χρειάζονται 0.81 bits για να κωδικοποιηθεί ένα μήνυμα που να επιλύσει την αβεβαιότητα της συνάρτησης μάζας πιθανότητας δηλώνοντας ποιο συμβάν συνέβη εν τέλει.

Είναι αναμενόμενο η εντροπία σε μία ομοιόμορφη συνάρτηση μάζας πιθανότητας να είναι μεγαλύτερη από μία ανομοιόμορφη αφού στην πρώτη περίπτωση δεν γνωρίζουμε τίποτα σχετικά με την πιθανή έκβαση ενώ στην δεύτερη περίπτωση έχουμε κάποια ιδέα (είναι πιο πιθανό να περάσει το μάθημα από το να μην το περάσει). Μάλιστα, σύμφωνα με την Aerin Kim στο άρθρο της The intuition behind Shannon’s Entropy ισχύει η εξής παρατήρηση: “Notice that in our example, with the “equally likely” messages, the entropy is higher (2 bits) than the “not equally likely” messages (0.81 bits). This is because there is less uncertainty in “not equally likely” messages. One event is more likely to come up than the other. This reduces the uncertainty.”

Στην ακραία περίπτωση που ο φίλος μας γνωρίζει πως σίγουρα θα περάσει το μάθημα (μία μόνο πιθανή έκβαση με 100% πιθανότητα επιτυχίας) η εντροπία είναι i=log₂1=0 bits που δηλώνει πως δεν χρειάζεται κανένα bit πληροφορίας για να επιλυθεί η αβεβαιότητα (αφού δεν υπάρχει αβεβαιότητα). Το ίδιο συμβαίνει όταν γνωρίζουμε σίγουρα πως ένα γεγονός δεν θα συμβεί. Αυτό συμβαίνει διότι όταν η πιθανότητα έκβασης ενός γεγονότος είναι 0%, η πιθανότητα μη έκβασης του είναι 100% και η εντροπία είναι και πάλι i=log₂1=0 bits.

Συνοψίζοντας τα παραπάνω, η εντροπία i μίας συνάρτησης μάζας πιθανότητας p(x) είναι η αβεβαιότητα, ή αλλιώς η έλλειψη πληροφορίας, του γεγονότος που περιγράφεται από αυτή την συνάρτηση p(x). Εάν εισάγουμε i ποσότητα πληροφορίας στις ήδη υπάρχουσες πληροφορίες για αυτό το συμβάν τότε η αβεβαιότητα λύνεται και γνωρίζουμε την τελική έκβαση του συμβάντος. Η εντροπία αφού εκφράζει την έλλειψη πληροφορίας μετριέται σε bits εάν ο λογάριθμος έχει βάση το 2 (δυαδικός λογάριθμος).

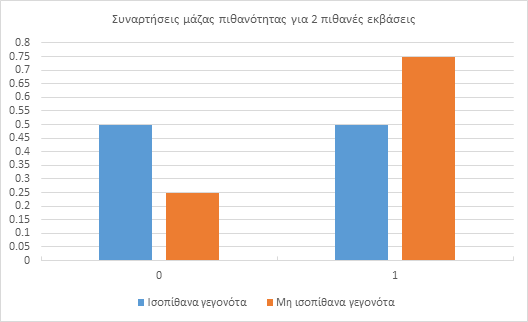
Τέλος, επισυνάπτονται οι γραφικές παραστάσεις των συναρτήσεων μάζας πιθανότητας που αναφέρθηκαν παραπάνω.